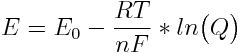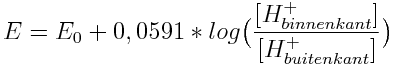pH theorie
Inhoudsopgave
pH definitie
pH beschrijft de hoeveelheid H+ kationen in een oplossing. Concentraties van deze ionen kunnen in een groot bereik variëren – meestal liggen waardes ergens tussen 1M en 10-14 M, maar soms kunnen er ook hogere of lagere waardes waargenomen worden.
Het gebruik van getallen die vele grootte ordes van elkaar verschillen is niet praktisch. Daarom ontwikkelde de Deense biochemicus Søren Sørensen in 1909 de pH-schaal en introduceerde hij de definitie van de pH als minus logaritme van 10 van [H+]:
Ofschoon de op deze manier gedefinieerde pH gebruikt kan worden voor eenvoudige pH-berekeningen in verdunde oplossingen van zuren en basen is dit niet helemaal correct. Het gedrag van ionen in de oplossing is niet afhankelijk van hun concentraties maar van hun activiteit. In het geval van sterk verdunde oplossingen (bijvoorbeeld minder dan 0,001M) kan het verschil tussen concentratie en activiteit worden verwaarloosd. In het geval van sterker geconcentreerde oplossingen moet er wel rekening mee gehouden worden. Er wordt dan ook gebruik gemaakt van een preciezere definitie:
Dit wordt soms ook wel de “thermodynamische pH” genoemd in tegenstelling tot de “concentratie pH”. Het is belangrijk om te weten dat alle pH-meters dynamische pH-waardes meten zoals die ook in de Vergelijking van Nernst staat.
pH schaal
De pH-definitie introduceert automatisch een pH-schaal. In de meeste waterige oplossingen bevindt de pH zich tussen 0 – 14 en vaak wordt aangenomen dat dit de grenzen zijn. Maar er zijn gevallen dat pH-waardes negatief of groter dan 14 zijn.
Waterige oplossingen bevatten altijd H+ en OH– -ionen die ofwel afkomstig zijn van autodissociatie van water of geïntroduceerd zijn door zuren of basen. Water dat dezelfde hoeveelheden van beide ionen bevat noemen we “neutraal”. In een neutrale oplossing geldt [H+ ]=[OH– ]=10-7 , dus een pH van een neutrale oplossing is 7 (dit kan, vooral bij hogere temperaturen, een beetje hoger zijn). Als een oplossing meer H+ dan OH– bevat dan is die oplossing acidisch en is de pH-waarde kleiner dan 7. Als er meer OH– dan H+ in de oplossing aanwezig is dan is de oplossing basisch en is de pH-waarde groter dan 7.
Deze pH-schaal wordt algemeen gebruikt want ze maakt het vergelijken van verschillende oplossingen of samples erg gemakkelijk. Bovendien geeft het vaak erg snel informatie over het sample. Het is veel gemakkelijker om te zeggen dat de pH van zeewater ongeveer 8 is dan te stellen dat de H+ -concentratie 10-8 M bedraagt. Daarnaast wetende dat zeewater een pH van 8 heeft zegt je dat het zeewater een beetje basisch is.
Om een beetje een gevoel te geven van de pH van verschillende stoffen:
| Substantie | pH-waarde |
|---|---|
| accuzuur | <1 |
| maagzuur | 2 |
| citroensap | 2,4 |
| melk | 6,5 |
| bloed | 7,34 – 7,45 |
| handzeep | 9 – 10 |
| bleekmiddel | 12,5 |
Merk op dat enkele waardes nauwkeuriger zijn weergegeven dan andere. De pH van bloed bijvoorbeeld wordt heel nauwkeurig door een koolzuurhoudende buffer binnen de gegeven range gehouden. Als de pH lager wordt dan leidt dit tot kortademigheid en als de pH te hoog wordt dan leidt dit tot ongewenste spiersamentrekkingen. De pH van ons maagzuur is afhankelijk van ons dieet en hoe lang het is geleden dat we voor het laatst hebben gegeten. De pH van zeep bevindt zich rond pH 9 tot 10 maar de natuurlijke pH van onze huid is licht acidisch (± pH 5). Dergelijke zeep maakt onze huid ruw en droog en dus passen meer en meer zeepfabrikanten de pH van hun zepen aan. De pH van citroensap is afhankelijk van de rijpheid van het fruit (de eerste pH-meters werden gemaakt voor de citroenteelt).
pH-berekeningen
Afhankelijk van het systeem kunnen pH-berekeningen erg gemakkelijk of extreem ingewikkeld zijn. Hier zijn drie redenen voor. Ten eerste, de meeste zuren en basen zijn zwak en om de concentratie H+ te berekenen met je het exacte equilibrium van het systeem weten – hoe meer componenten er aanwezig zijn hoe meer interacties er plaatsvinden waarmee rekening gehouden moet worden en hoe lastiger de berekeningen worden.
Ten tweede is water als gevolg van autodissociatie zelf een bron van H+ ionen en die spelen een belangrijke rol in verdunde oplossingen van zuren en basen (dat is ook de reden dat zuiver water pH = 7 heeft).
Ten derde, in het geval van meer geconcentreerde oplossingen (> 0,01M of zelfs > 0,001M) speelt de activiteit een grote rol en dat zorgt ook voor ingewikkeldere berekeningen.
In het geval van een verdund, meer niet sterk verdund, sterk zuur, zoals bijvoorbeeld zoutzuur, kunnen we aannemen dat de activiteit van H+ gelijk is aan de concentratie en dat het zuur volledig is gedissocieerd. Dus de pH van een 10-4 M HCl-oplossing is:
Echter, als deze oplossing sterk is verdund, bijvoorbeeld tot 10-7 M, dan is deze eenvoudige benadering niet voldoende want de pH van de oplossing is niet 7 maar 6,79. Dit wordt veroorzaakt door de H+ afkomstig van de dissociatie van water.
In het geval van een zwak zuur (azijnzuur bijvoorbeeld) moet je naast de autodissociatie van water ook rekening houden met de evenwichtsconstante voor de dissociatie. In het algemeen leidt dit tot een derdemachtsvergelijking die in de meeste gevallen vereenvoudigd kan worden tot een kwadratische vergelijking. Dit komt omdat de zuurconcentratie meestal groot genoeg is om de dissociatie van water te negeren.
De Vergelijking van Nernst
De Vergelijking van Nernst beschrijft de potentiaal van een elektrochemische cel als functie van de concentratie ionen die deelnemen in de reactie:
In deze vergelijking is Q het reactie quotiënt en n het aantal elektronen dat wordt uitgewisseld. Bij een constante temperatuur heeft RT/F een constante waarde. Om de berekeningen te vereenvoudigen wordt deze vaak gecombineerd met een conversiefactor tussen de natuurlijke logaritme (ln) en de decimale logaritme (log) tot de waarde van 0,0591 (bij een temperatuur van 25 °).
Laten we eens kijken naar het volgende voorbeeld: MnO4 – + 8H+ + 5e– → Mn2+ + 4H2 O
De potentiaal wordt gegeven door:
Om dit goed te doen zouden we geen concentraties moeten gebruiken maar de thermodynamische activiteit van de ionen die in de oplossing aanwezig zijn.
Wanneer toegepast op een volledige cel die uit halve cellen bestaat op de binnenkant en de buitenkant van een glazen pH elektrode dan ziet de Vergelijking van Nernst er als volgt uit:
of (gebruikmakende van de pH-definitie):
De pH van de binnenkant van de elektrode heeft een constante waarde dus die kan in het potentiaal deel van de vergelijking worden opgenomen:
Deze vorm van de vergelijking beschrijft het gedrag van de glaselektrode die wordt gebruikt voor pH-metingen. Twee opmerkingen zijn hier nog van belang.
- Bovenstaande vergelijking gaat uit van een ideale respons van de glaselektrode.
- De waarde van 0,0591 is berekend voor een temperatuur van 25°C.
In de meeste gevallen gedragen elektrodes zich niet ideaal en is de temperatuur niet precies 25 °C dus zal de slope van de elektroderespons niet 0,0591 zijn. Om deze problemen te omzeilen moet er voor iedere meting of serie van metingen gekalibreerd worden.